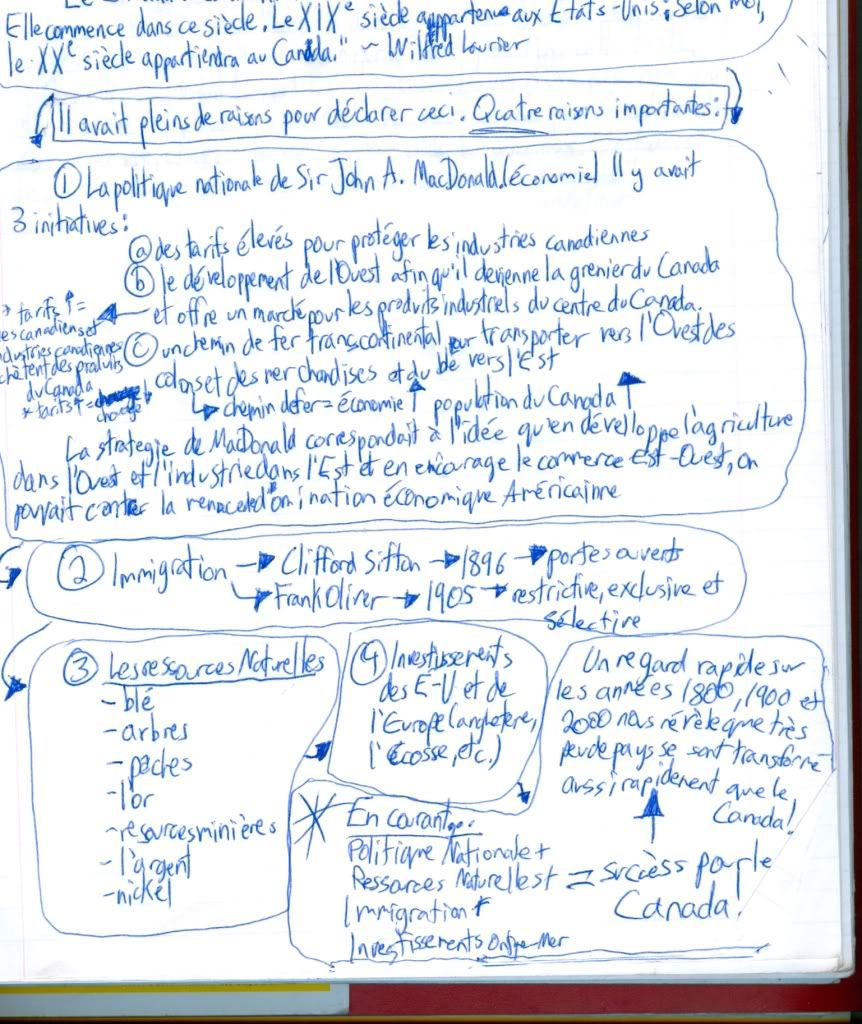
Perihelion
Sponsor
Some people say that you can tell a lot about a person by how they write, and while I think handwriting analysis is a load of shit, it's still kind of interesting to compare. So post pictures/scans/whatever!
Unfortunately the only good-sized bit of writing I have on hand is my math notes, so bear with me here. Apologies for the shitty picture:

"Green's Theorem
Provides a link between line integrals and double integrals. It takes up the question of whether (the partial derivative of M with respect to x) = (the partial derivative of N with respect to y) is sufficient to guarantee that F is conservative (i.e. if integral around every closed path is 0).
If C is a piecewise smooth closed curve that bounds a region R, and if M(x,y) and N(x,y) are continuous and have continuous partial derivatives along C and throughout R, then
(the line integral over the closed curve C) Mdx + Ndy = (the double integral over the region R) (partial derivative of N with respect to x) - (partial derivative of M with respect to y) dA
(blobby thing with R in the middle and C and an arrow on the outside) C is a simple closed curve, and R is the interior."
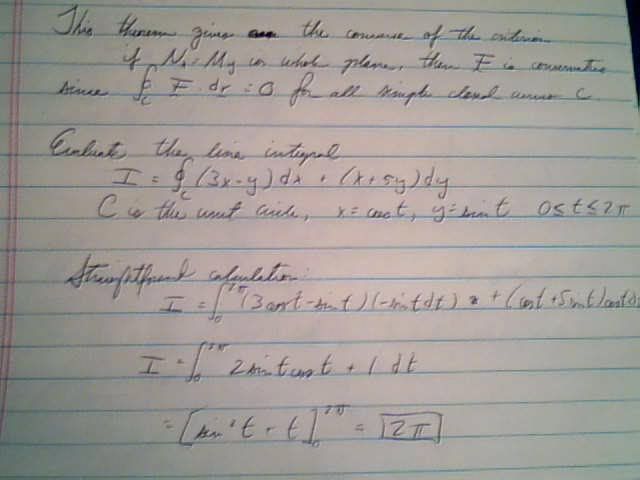
"This theorem gives the converse of the criterion.
if Nx = My in whole plane, then F is conservative
since (the line integral over the closed curve C) F dotted with dr = 0 for all simple closed curves C.
Evaluate the line integral
I = (the line integral over the closed curve C) (3x - y)dx + (x + 5y)dy
C is the unit circle, x = cost, y = sint, 0 <= t <= 2pi
Straightforward calculation:
I = (the integral from 0 to 2pi) (3cost - sint)(-sint dt) + (cost + 5sint)(cost dt)
I = (the integral from 0 to 2pi) 2sintcost + 1 dt
= [sin^2t + t] evaluated from 0 to 2pi = 2pi"
Apologies for math, but I was too lazy to write up something else! @_@
Unfortunately the only good-sized bit of writing I have on hand is my math notes, so bear with me here. Apologies for the shitty picture:

"Green's Theorem
Provides a link between line integrals and double integrals. It takes up the question of whether (the partial derivative of M with respect to x) = (the partial derivative of N with respect to y) is sufficient to guarantee that F is conservative (i.e. if integral around every closed path is 0).
If C is a piecewise smooth closed curve that bounds a region R, and if M(x,y) and N(x,y) are continuous and have continuous partial derivatives along C and throughout R, then
(the line integral over the closed curve C) Mdx + Ndy = (the double integral over the region R) (partial derivative of N with respect to x) - (partial derivative of M with respect to y) dA
(blobby thing with R in the middle and C and an arrow on the outside) C is a simple closed curve, and R is the interior."
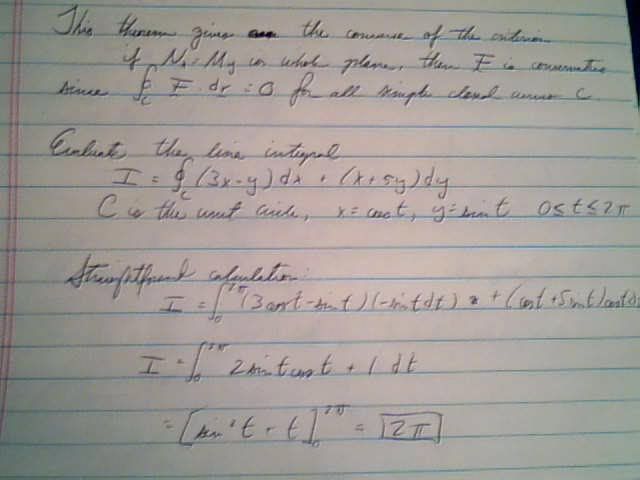
"This theorem gives the converse of the criterion.
if Nx = My in whole plane, then F is conservative
since (the line integral over the closed curve C) F dotted with dr = 0 for all simple closed curves C.
Evaluate the line integral
I = (the line integral over the closed curve C) (3x - y)dx + (x + 5y)dy
C is the unit circle, x = cost, y = sint, 0 <= t <= 2pi
Straightforward calculation:
I = (the integral from 0 to 2pi) (3cost - sint)(-sint dt) + (cost + 5sint)(cost dt)
I = (the integral from 0 to 2pi) 2sintcost + 1 dt
= [sin^2t + t] evaluated from 0 to 2pi = 2pi"
Apologies for math, but I was too lazy to write up something else! @_@